
Interview
de Vincent Surdyk
Professeur des écoles, directeur d’école puis coordonnateur REP, il a également été enseignant référent pour les usages du numérique.
Depuis 2018, il est conseiller pédagogique et référent en mathématiques de circonscription.
Il a créé la démarche collaborative
Les Dioramaths et est auteur du compte Instagram @super_maths_story
Auteur de
Debloki - Résolution de problèmes NOUVEAU
Ateliers Décomposition du nombre 1 & 2 NOUVEAU
Atelier B-A BA des motifs NOUVEAU
Comment vous est venue l’idée de concevoir Debloki - Résolution de problèmes ? Qu’ont apporté les tests dans plus de 100 classes ?
L’idée m’est venue lors de formations sur le rôle essentiel du matériel de manipulation dans la résolution de problèmes. Avant de passer à des formes de schématisation au cycle 2, il est indispensable que l’élève manipule les nombres pour comprendre les relations entre eux. J’ai constaté qu’aucun matériel n’existait pour vraiment préparer à comprendre ces relations.
Après avoir analysé les outils disponibles, j’ai conçu mes premiers prototypes avec mon imprimante 3D dans mon garage. Je voulais y intégrer la ligne numérique, appui reconnu dans les programmes de cycles 1 et 2. Debloki est né ainsi, avec ses lignes numériques pour placer les blocs nombres. En classe, les élèves se concentraient tout de suite sur les liens entre les données, manipulaient facilement et résolvaient les problèmes sans être bloqués par le calcul. Les justifications des élèves associées à leurs manipulations permettaient aux enseignant(e)s d’aider les élèves à résoudre des problèmes arithmétiques en maternelle.
Vous expérimentez quotidiennement que les enfants prennent du plaisir à résoudre des problèmes arithmétiques dès la maternelle. Quelles sont les clés de leur envie et leur motivation ?
Les enfants ont naturellement envie de faire des maths, c’est aussi lié à une forte culture de la manipulation dès la maternelle. Ils aiment beaucoup ce qui touche aux nombres car ils ressentent une forme de codage du monde qui les entoure. C’est instinctif.
Dans la résolution de problèmes, il apparaît un point crucial, celui de la recherche d’une réponse, d’une solution qui n’est pas disponible tout de suite, alors il faut la trouver et les enfants adorent chercher. Pour les problèmes arithmétiques, les enfants adorent quand on leur lit l’énoncé du problème ou plutôt « de la petite histoire ». Ce que j’aime appeler « les histoires mathématiques ». Il faut faire comprendre à l’enfant que quelque chose est à trouver, quelque chose de caché. C’est de là que tout part, l’envie de chercher. Cette quête est cruciale et doit faire l’objet de toutes les attentions, j’aime la théâtraliser, montrer que je cache des choses pour attiser leur curiosité et leur engagement dans l’activité.
Et les points de vigilance pour les enseignant(e)s ?
Le premier point de vigilance concerne le matériel utilisé en classe pour résoudre des problèmes. Au départ on utilisera toujours du matériel figuratif, puis on passera à des jetons et des cubes pour enfin aborder des barres cardinales par exemple ou les blocs nombres de Debloki. Le matériel de classe est un puissant outil pour construire des savoirs mathématiques à condition que ce matériel soit « transparent ». Cela signifie qu’il doit permettre d’accéder clairement au concept qu’il représente. Ainsi on expliquera aux enfants le sens des représentations cardinales du matériel, pour cela on pourra s’appuyer sur les décompositions des nombres.
Le second point de vigilance est d’introduire la ligne numérique le plus tôt possible. Elle est un support puissant pour comprendre comment les nombres s’organisent, s’ordonnent et se construisent. Chaque valeur cardinale a son importance sur la ligne numérique.
Il est très important également de bien formaliser avec les enfants ce qu’il faut trouver dans le problème (ou l’histoire). Cela parait évident, mais les enfants ont besoin de se concentrer sur ce point pour construire une stratégie de recherche.
Enfin, je dirai qu’il faut surtout laisser les élèves chercher et ne pas intervenir. Chacune de leur action, de leur manipulation ou de leur schématisation sera ensuite l’objet d’échange avec l’enseignant(e). Le matériel est un support efficace pour exploiter le travail de l’enfant et lui parler. Pour les enfants ayant atteint un niveau d’abstraction supérieur, ce sont les dessins ou schémas qui serviront d’appui même si le matériel peut être utilisé pour ceux qui n’arrivent pas à dire comment ils ont fait « dans leur tête ».
Debloki matérialise de manière astucieuse la chronologie des énoncés de problèmes et la manipulation des nombres des énoncés. Pouvez-vous nous en dire plus ?
La chronologie des énoncés est un point très important pour construire une réflexion sur les relations entre les nombres de l’énoncé. Quand l’élève écoute un énoncé de problème, il commence à entendre des nombres et les met en mémoire. Tout l’enjeu est de comprendre comment se servir de cette mémorisation pour construire une relation mathématique. C’est ici que Debloki va aider les enfants.
Les fiches d'énoncés de problèmes comportent une face avec le texte écrit pour la lecture et une face imagée représentant les différentes phases de l’énoncé. Ce n’est pas une représentation de la démarche de résolution mais un focus pour aider les élèves à construire la filiation entre les nombres en jeu. Sur la fiche, on focalise également sur ce qui est à chercher.

Les fiches sont un puissant élément de différenciation et de remédiation pour les enfants qui ont besoin de se remémorer et de reformuler l’histoire. Ils aiment beaucoup s’en servir en racontant eux-mêmes l’énoncé. C’est un moyen de les aider à produire à l’oral un énoncé mathématique. L’accompagnement par l’enseignant(e) est essentiel.
Enfin les différentes fiches offrent des représentations spécifiques par types de problèmes pour aider les élèves à construire une modélisation.
Debloki peut facilement être manipulé pendant que le problème est lu. Chaque manipulation demande un contrôle par l’enfant de ce qui se passe dans l’énoncé, et cela est facilité par la consultation des fiches d'énoncés de problèmes.
Que faire avec un enfant qui bloque sur la compréhension d’un problème ? Quels conseils donneriez-vous ?
Dans un premier temps, il faut vérifier que l’élève a bien construit le sens des manipulations avec du matériel concret comme, par exemple, des personnages, des jetons ou des cubes. Vérifier que l’enfant sait ajouter, retirer et partager du matériel. Cela peut être fait en dehors d’une activité de résolution de problème pour éviter la surcharge cognitive.
Ensuite, toujours avec du matériel concret si besoin, l’enseignant guidera l’enfant en lui proposant des histoires mathématiques (énoncés) où toutes les actions de manipulation sont visibles. L’enseignant fera observer à l’enfant ce qui se passe dans l’énoncé sans cacher ce qu’il faut chercher. L’enfant a parfois besoin de comprendre comment les nombres évoluent et où se trouvent les quantités en jeu une fois l’action terminée. C’est un travail d’explicitation très important qui va conduire progressivement vers l’abstraction.
Durant tout cet accompagnement, il faut veiller à faire verbaliser l’enfant. Chaque manipulation doit être accompagnée et justifiée pour prendre le temps de consolider les relations entre les nombres de l’énoncé qui conduiront ensuite aux opérations.
Le langage et la manipulation sont les clés pour résoudre les problèmes avec Debloki.
Découvrez Debloki - Résolution de problèmes

 NOUVEAU
NOUVEAU
Un outil pour faire manipuler les nombres des énoncés et aider les élèves à comprendre les problèmes arithmétiques.
Comment ça marche ?
1. On lit l’énoncé du problème de haut en bas, étape par étape.
Exemple : problème d’ajout - recherche de l’état final
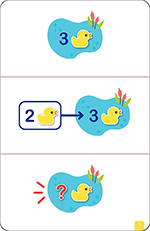
« Il y a 3 canards dans une mare. »
« 2 nouveaux canards arrivent dans la mare. »
« Combien y a-t-il de canards en tout dans la mare ? »
2. On manipule les blocs nombres dans le plateau, en suivant la chronologie de l’histoire.

3. On trouve la réponse en lisant sur la droite numérique.
La démarche de recherche et de résolution des problèmes met en avant :
- la chronologie des énoncés,
- la manipulation concrète des nombres,
- la verbalisation des stratégies.
Différentes modalités de travail sont possibles : en atelier guidé de 6 à 8 élèves, en atelier autonome collaboratif de 2 à 3 élèves, en atelier autonome individuel.
À découvrir aussi
ATELIERS DÉCOMPOSITION DU NOMBRE
Très ludiques, ces ateliers développent les compétences de composition-décomposition des nombres jusqu’à 10. Ils mettent en avant la manipulation de SmartCubes (une exclusivité Nathan !), la verbalisation des procédures, la mémorisation, et développent les premières stratégies de calcul (surcomptage, etc.).
Atelier Décomposition du nombre 1 - De 1 à 6
 NOUVEAU
NOUVEAU
Atelier Décomposition du nombre 2 - De 7 à 10
 NOUVEAU
NOUVEAU
ATELIERS RÉSOLUTION DE PROBLÈMES - NUMÉRATION
Les situations-problèmes amènent les enfants à utiliser spontanément les nombres. Les activités font appel au questionnement, à la réflexion, à la recherche de procédures efficaces de résolution des différents types de problèmes par essais-ajustements.
Atelier Résolution de problèmes - Numération 1

Atelier Résolution de problèmes - Numération 2

LES DÉFIS MHM

Des outils clés en main pour mettre en place des rallyes mathématiques et résoudre des problèmes en équipes. La démarche valorise le plaisir de la recherche, la coopération entre élèves, et donne une place très importante au langage. Tous les défis ont été testés en classe.
12 défis à relever en équipes - À la mer

 NOUVEAU
NOUVEAU
12 défis à relever en équipes - Dans la forêt

12 défis à relever en équipes - Au fil des saisons

LES BOÎTES À ÉNIGMES MHM

Chaque boîte contient 30 énigmes en images, inspirées de la vie quotidienne, pour exploiter les connaissances mathématiques et s’entraîner à la résolution de problèmes. 3 niveaux de questions à chaque énigme + les QR codes pour accéder aux audios des questions et des réponses.
La boîte à énigmes - Cycle 1



La boîte à énigmes 2 - Cycle 1



 FR
FR Learning Materials
Learning Materials












